When the brake pedal of a car moving 80 km/h on a straight asphalt road is fully pressed, the car can stop in 50 m. How long will its braking distance be on an identical road which forms a 5° angle with the horizontal plane? Consider both the case when it brakes downhill and when it brakes uphill. Assume that at the time t = 0 s the coordinate is x = 0 m. The wheels do not slip. Neglect the air resistance.
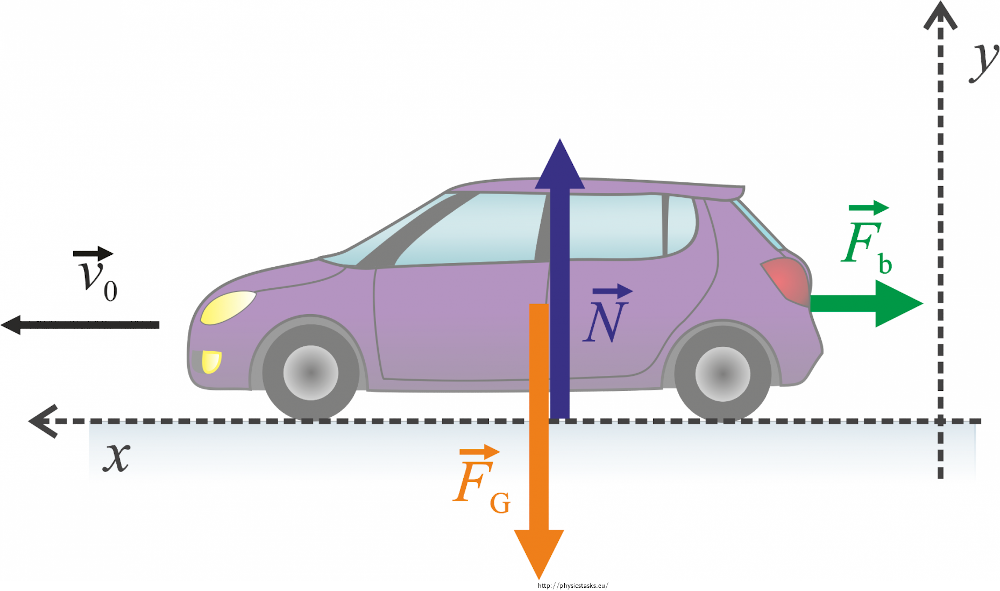
Please enter the following data to calculate the previous equation
Enter m
Enter s
Enter v
Enter α
We express force N from relation (14) and substitute for it
We substitute for f from relation to (12)
Enter Fb
Enter g
Enter m
Enter α
We evaluate acceleration from equation (13)
Enter m
Enter g
Enter Fb
Enter t
Enter α
If we rewrite equation (17), we obtain the dependency of the velocity of the car velocity on time
By integrating relation (18) we obtain the dependency of the coordinate time
Enter m
Enter t
Enter Fb
Enter α
If we rewrite equation (19), we obtain the dependency of the dependency of the coordinate of the car on time
We calculate the time of stopping t1 by substituting zero for velocity into relation (18)
Enter Fb
Enter m
Enter g
Enter v
Enter α
We substiyute the time t1 into relation (20) and calculate the total distance Ss travelled by the car
Enter g
Enter s
Enter v
Enter α
We substitute for Fb into relation (15)
Enter m
Enter g
Enter v
Enter Ss
.
Enter Ts2
Enter Fb2
Enter m
Enter g
Enter α
.
Enter Fb2
Enter m
Enter g
Enter α
Enter Ts2
.
Enter Fb2
Enter m
Enter g
Enter v0
Enter α
.
Enter m